I wrote the below post for Tencap back in July of 2012, just after Roger won his 7th Wimbledon title. Nobody ever read it, and I doubt anyone will read it here either, but I figured this new site needed at least one post, so I decided to re-purpose the old one here.
Roger Federer’s recent return to #1 in the rankings – his 287th week as world #1 as of 7/16/2012, a new record in his impressive list of records – along with his record tying 7th Wimbledon title and record-extending 17th major title overall, has had the effect of further widening the gap between himself and the rest of the field of GOAT-worthy contenders. Since his loss to Djokovic in the 2011 US Open semi-finals, Federer has shown us that there simply isn’t any rational way to argue that he isn’t the greatest of all time.
You may recall that back in March I created an ordered list of the greatest (male) tennis players of all time which showed that statistically speaking, Roger Federer is the greatest of all time (GOAT). The general idea behind the ranking “algorithm” was to pick multiple GOAT-worthy categories – grand slams won, titles won, weeks at #1, etc. – and then average the players ranking in each category to find out who had the lowest average across all categories; i.e., who was closest to #1 overall. For example, if there were two categories and a player was ranked #1 in both, his average would be 1.0. If there were two categories and a player was ranked first in one, and second in another, his average would be 1.5. You get the idea.
Also, since I had different ideas for the criteria, I created three different “what if” lists, adding additional criteria to the 2nd and 3rd lists in order to see what effect those criteria had on a player’s ranking. Here are the criteria for each of the three lists (left hand column) along with the number one player in each category:
|
GOAT Criteria |
|||
|
#1) GS Titles |
Federer |
Federer |
Federer |
|
#2) GS Finals |
Federer |
Federer |
Federer |
|
#3) GS Surfaces* |
(see notes) |
||
|
#4) Total Wins |
Connors |
Connors |
Connors |
|
#5) Titles |
Connors |
Connors |
Connors |
|
#6) Finals |
Federer |
Federer |
Federer |
|
#7) Weeks #1 |
Federer |
Federer |
Federer |
|
#8) Consecutive Weeks #1 |
Federer |
Federer |
Federer |
|
#9) Masters Wins |
N/A |
Nadal |
Nadal |
|
#10) Olympics* |
N/A |
N/A |
(see notes) |
*Note* Both the GS Surfaces category (a ranking of the number of different surfaces a player has won a grand slam on. Both Federer and Nadal have won on all four surfaces placing them in a seven-way tie for first with Perry, Budge, Laver, Emerson, and Agassi) and the Olympics (Gold is #1, Silver #2, Bronze #3) are capable of having multiple players with a #1 ranking. Every other category is a true list with clear rankings for first, second, third, and so on.
As you can see, Federer owns five of the records outright, and shares a sixth (GS Surfaces) with Perry, Budge, Laver, Emerson, Agassi, and Nadal. In fact, I added Masters Wins and the Olympics precisely because I knew those are (at the time of writing) categories Federer didn’t own.
Anyway, I received mostly positive feedback about the effort, but there were a few people who noticed problems. Some problems were minor, such as not giving a player his due credit for a given category. Barbara, for example, provided some good feedback in her comment on 6/30/2012
But may I point out a couple of small things? Ilie Nastase won GSs on 2 surfaces, not just one: the USO (Forest Hills) in 1972 on grass (!), and the FO in 1973 on clay. So he should have a 3, not a 4, in that category. He also won the hardcourt indoor Masters – now the WTF – 4 times, which sadly is not counted here at all. So arguably he should be higher than No 13!
Other problems were more significant, and Andrew Ross highlighted the biggest flaw when he pointed out, “Rankings can’t be averaged as you’re doing. They’re ordinal statistics. Also: Not all your categories are equivalent.”
In other words (via Statistics Glossary):
A set of data is said to be ordinal if the values / observations belonging to it can be ranked (put in order) or have a rating scale attached. You can count and order, but not measure, ordinal data. [my emphasis]
So, he’s right. Sort of. But only in the most important aspect of what I’m trying to do. That said, it was never my intent to measure, as I didn’t know how to do it, and more importantly, I didn’t think it even could be done. (And then later, I learned that it actually cannot be done1.) To better illustrate the problem we have (see how I’m dragging you into it now), we’re going to need to return to your middle school science class.
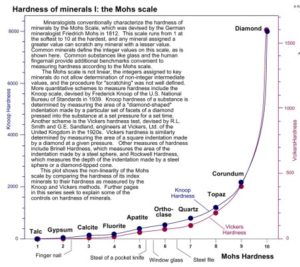
As you may recall, minerals can be ranked according to their hardness. The softest is talc whereas the hardest known mineral is, of course, diamond. If we were to create a HOAT (Hardest of All Time) list of minerals, it’d look like this: (with 1 being the softest and 10 being the hardest)
| Hardness Ranking | Mineral | Mohs Ranking |
| 1 | Diamond | 10 |
| 2 | Corundum | 9 |
| 3 | Topaz | 8 |
| 4 | Quartz | 7 |
| 5 | Feldspar | 6 |
| 6 | Apatite | 5 |
| 7 | Fluorite | 4 |
| 8 | Calcite | 3 |
| 9 | Gypsum | 2 |
| 10 | Talc | 1 |
OK, so how close is corundum, the 2nd hardest mineral on this list, to diamond?. Looking at this list one would think that corundum is almost as hard as diamond since it’s just one ranking away. Unfortunately, one would be wrong. Compared to diamond, corundum is in the minor leagues of hardness. In tennis terms, it’s somewhere in the Challengers circuit; nowhere near the diamond level of the ATP. Here’s a graphic that shows what the real gap is between corundum and diamond:
As you can see, it’s not even close. And the reason for the false sense of parity is exactly what Andrew Ross was getting at, and the same reason it’s not entirely accurate to call Federer the GOAT: the ranked list does not show you the magnitude of the criteria being evaluated.

Which is why it’s not entirely accurate to say Federer is the Greatest of All Time: Federer’s not just the Greatest Of All Time, he’s the Greatest Of All Time by a long shot.
Consider this: In the entire history of tennis, there have only been 51 players win 3 or more grand slams. And with seventeen trophies, Federer has three more than the next closest player, Pete Sampras, who in turn has three more than players like Borg, Laver, and Nadal! Let that sink in for a bit. Federer has six(!) more titles than Rod “I have a stadium named after me in Australia” Laver. In the entire history of tennis, there have only been 26 players win six or more grand slams. If Sampras is in rarified air, Federer is in low earth orbit.
Too important to be relegated to a footnote: None of this is in any way a slam against any other player. Although I am a huge Federer fan and will always be rooting for him to win, my respect for him is not mutually exclusive with my respect for any other player. This is to say that I’m not a “hater” of Nadal, or Djokovic, or Murray, or any other player for that matter. And I’ll go a step further and say that if your passion for Player A comes at the expense of Player B, I judge you in a very unfavorable way. I read comments by the haters, and find them telling. If you’re a hater, I probably will not respect your opinion.
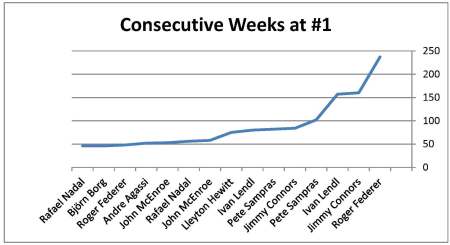
Also, recognize that I have not included the record 32 semi-finals, the record 23 straight semi-finals, the record 33 straight quarterfinals, or the record 10 straight finals. Nor did I include the 237 consecutive weeks at #1. That’s 77 weeks more than the 2nd place contender, Jimmy Connors.2 These are records that may never be achieved again in men’s tennis and are in and of themselves GOAT-worthy criteria. What would it look like if I had included them?
It’d look like Federer was the Greatest Of All Time. By a long shot.
Are there problems with this ranking scheme? Yes. Do they prevent us from accomplishing what we set out to do? No, far from it. In fact, if nothing else, at least this method provides *an* objective framework with which to answer the question. For example, how many wins does Nadal need in order to make it to the #10 spot in the “Total Wins” category? A: With 583 wins, Nadal needs to win 91 more matches to displace Brian Gottfried from the #10 spot on the all-time-wins list. How many wins does Federer need to displace John McEnroe from the #4 spot on the “Total Wins” list? A: 23.
How important is an Olympic gold medal to Federer? Look at the list; it’s hugely important to him.
Notes:
- From Scientific American, July, 2012: “In 1951 Kenneth Arrow, a mathematical economist, proved that there can be no optimal ranking system that also satisfies certain fairness criteria. Thus, the controversy lives on, keeping raters and rankers in business by continually tweaking and tailoring their systems to fit specialized needs.”
- From ATP Grand Slam Tournament Records (Wikipedia)